| Home | Trees | Indices | Help |
|
|---|
|
|

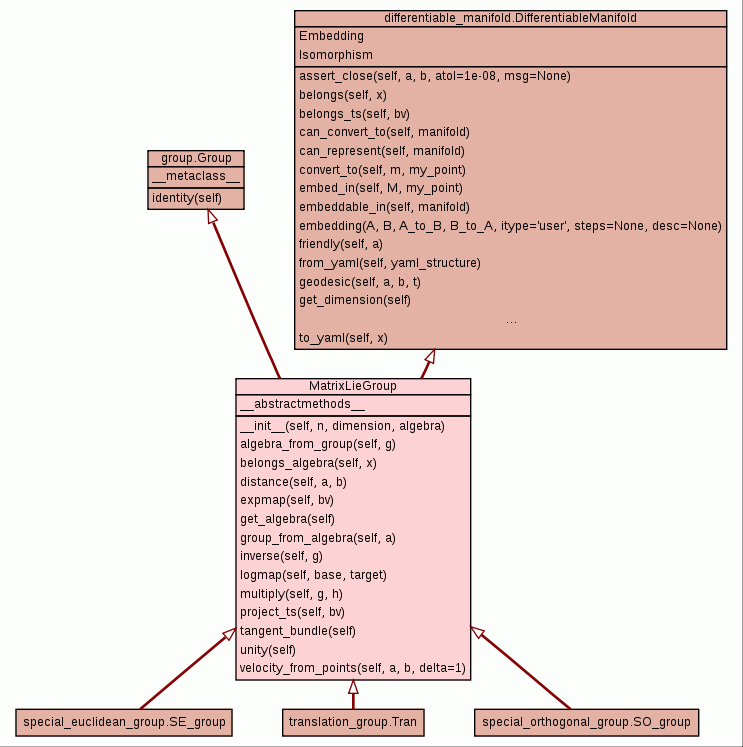
This is the base class for matrix Lie groups.
Subclasses should provide a MatrixLieAlgebra object. Given the Lie algebra, we can compute everything. However, subclasses can choose to overload some functions if they know a more numerically stable implementation.
|
|||
|
Inherited from Inherited from |
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
Inherited from Inherited from Inherited from |
|||
|
|||
|
Inherited from |
|||
|
|||
__abstractmethods__ = |
|||
_abc_cache = <_weakrefset.WeakSet object at 0x23ad910>
|
|||
|
Inherited from |
|||
|
|||
|
Inherited from |
|||
|
|||
Initializes the Lie group. :param n: dimension of the matrix group. :param algebra: instance of :py:class:MatrixLieAlgebra
|
Converts an element of the group to the algebra.
Uses generic matrix logarithm plus projection.
:param g:
:type g: ``belongs``
:rtype: ``belongs_algebra``
|
Computes the distance between two points.
In the case of Lie groups, this is done by
translating everything to the origin, computing the
logmap, and using the norm defined in the Lie Algebra object.
:param a:
:type a: ``belongs``
:param b:
:type b: ``belongs``
|
This is the inverse of :py:func:`logmap_`.
In the case of Lie groups, this is implemented using
the usual matrix exponential.
Here the :py:func:`MatrixLieAlgebra.project` function
is used to mitigate numerical errors.
:param bv:
:type bv: ``belongs_ts``
:rtype: ``belongs``
|
Converts an element of the algebra to the group.
Uses generic matrix exponential.
:param a:
:type a: ``belongs_algebra``
:rtype: ``belongs``
|
:param g: :type g: ``belongs`` :rtype: ``belongs``
|
Returns the direction from base to target.
In the case of Lie groups, this is implemented
by using the usual matrix logarithm at the origin.
Here the :py:func:`MatrixLieAlgebra.project` function
is used to mitigate numerical errors.
:param base:
:type base: ``belongs``
:param target:
:type target: ``belongs``
:rtype: ``belongs_ts``
|
:param h: :type h: ``belongs`` :param g: :type g: ``belongs``
|
Projects the vector *x* to the tangent space at point *base*.
In the case of Lie Groups, we do this by translating the
vector to the origin, projecting it to the Lie Algebra,
and then translating it back.
:param bv:
:type bv: ``tuple(belongs,*)``
|
Returns the manifold corresponding to the tangent bundle. The default gives a generic implementation. MatrixLieGroup have a different one.
|
Returns the group unity.
|
Find the velocity in local frame to go from *a* to *b* in
*delta* time.
:param a:
:type a: ``belongs``
:param b:
:type b: ``belongs``
:rtype: ``belongs_ts``
|
| Home | Trees | Indices | Help |
|
|---|
| Generated by Epydoc 3.0.1 on Wed Feb 22 20:39:22 2012 | http://epydoc.sourceforge.net |