geometry package

Subpackages

Submodules

geometry.basic_utils module

geometry.basic_utils.deprecated(func)[source]

This is a decorator which can be used to mark functions as deprecated. It will result in a warning being emitted when the function is used.

geometry.basic_utils.finite(x)[source]
geometry.basic_utils.normalize_length(s, norm=2)[source]

Normalize an array such that it has unit length in the given norm.

geometry.basic_utils.normalize_length_or_zero(s, norm=2)[source]

Normalize an array such that it has unit length in the given norm; if the norm is close to zero, the zero vector is returned.

geometry.basic_utils.safe_arccos(x)[source]

Returns the arcosine of x, clipped between -1 and 1.

Use this when you know x is a cosine, but it might be slightly over 1 or below -1 due to numerical errors.

geometry.constants module

class geometry.constants.GeometryConstants[source]

Bases: object

atol_zero_norm = 1e-07
rtol_SE2_from_SE3 = 0.0001

geometry.formatting module

geometry.formatting.add_spacer(cols, spacer=' ')[source]
geometry.formatting.format_matrix(matrix, fsize=8, format_str='%g')[source]
geometry.formatting.formatm(*args, **kwargs)[source]
geometry.formatting.join_columns(cols)[source]
geometry.formatting.printm(*args)[source]

geometry.mds_algos module

geometry.mds_algos.best_embedding_on_sphere(C, ndim, embed=<function inner_product_embedding>)
geometry.mds_algos.double_center(P)[source]
geometry.mds_algos.euclidean_distances(S)[source]

Computes the euclidean distance matrix for the given points.

geometry.mds_algos.inner_product_embedding(C, ndim)[source]
geometry.mds_algos.inner_product_embedding_randomized(C, ndim)[source]

Best embedding of inner product matrix based on randomized projections.

geometry.mds_algos.inner_product_embedding_slow(C, ndim)[source]
geometry.mds_algos.mds(D, ndim, embed=<function inner_product_embedding>)[source]
geometry.mds_algos.mds_randomized(D, ndim)[source]

MDS based on randomized projections.

geometry.mds_algos.place(references, distances)[source]
geometry.mds_algos.spherical_mds(C, ndim, embed=<function inner_product_embedding>)[source]
geometry.mds_algos.truncated_svd_randomized(M, k)[source]

Truncated SVD based on randomized projections.

geometry.poses module

geometry.poses.SE2_from_SE3(pose, check_exact=True, z_atol=1e-06)[source]

Projects a pose in SE3 to SE2.

If check_exact is True, it will check that z = 0 and axis ~= [0,0,1].

geometry.poses.SE2_from_rotation_translation(R, t)
geometry.poses.SE2_from_se2(vel)[source]

Converts from Lie algebra representation to pose.

See Bullo, Murray “PD control on the euclidean group” for proofs.

geometry.poses.SE2_from_se2_slow(vel)[source]
geometry.poses.SE2_from_translation_angle(t, theta)[source]

Returns an element of SE2 from translation and rotation.

geometry.poses.SE2_from_xytheta(xytheta)[source]

Returns an element of SE2 from translation and rotation.

geometry.poses.SE2_identity()[source]
geometry.poses.SE3_from_SE2(pose)[source]

Embeds a pose in SE2 to SE3, setting z=0 and upright.

geometry.poses.SE3_from_rotation_translation(R, t)
geometry.poses.SE3_identity()[source]
geometry.poses.angle_from_SE2(pose)[source]
geometry.poses.angular_from_se2(vel)[source]
geometry.poses.check_SE(M)[source]

Checks that the argument is in the special euclidean group.

geometry.poses.check_se(M)[source]

Checks that the input is in the special euclidean Lie algebra.

geometry.poses.combine_pieces(a, b, c, d)[source]
geometry.poses.extract_pieces(x)[source]
geometry.poses.linear_angular_from_se2(vel)[source]
geometry.poses.pose_from_rotation_translation(R, t)[source]
geometry.poses.rotation_translation_from_SE2(pose)
geometry.poses.rotation_translation_from_SE3(pose)
geometry.poses.rotation_translation_from_pose(pose)[source]
geometry.poses.se2_from_SE2(pose)[source]

Converts a pose to its Lie algebra representation.

See Bullo, Murray “PD control on the euclidean group” for proofs.

geometry.poses.se2_from_SE2_slow(pose)[source]

Converts a pose to its Lie algebra representation.

geometry.poses.se2_from_linear_angular(linear, angular)[source]

Returns an element of se2 from linear and angular velocity.

geometry.poses.translation_angle_from_SE2(pose)[source]
geometry.poses.translation_from_SE2(pose)[source]
geometry.poses.translation_from_SE3(pose)[source]
geometry.poses.xytheta_from_SE2(pose)[source]

Returns an element of SE2 from translation and rotation.

geometry.poses_embedding module

geometry.poses_embedding.R2_project_from_SE2(b)[source]
geometry.poses_embedding.R3_project_from_SE3(b)[source]
geometry.poses_embedding.SE2_from_R2(a)[source]
geometry.poses_embedding.SE2_from_SO2(a)[source]
geometry.poses_embedding.SE2_project_from_SE3(b)[source]
geometry.poses_embedding.SE3_from_R3(a)[source]
geometry.poses_embedding.SE3_from_SO3(a)[source]
geometry.poses_embedding.SO2_project_from_SE2(b)[source]
geometry.poses_embedding.SO3_project_from_SE3(b)[source]
geometry.poses_embedding.se2_from_so2(a)[source]
geometry.poses_embedding.se2_project_from_se3(b)[source]
geometry.poses_embedding.se3_from_se2(a)[source]
geometry.poses_embedding.se3_from_so3(a)[source]
geometry.poses_embedding.so2_project_from_se2(b)[source]
geometry.poses_embedding.so3_project_from_se3(b)[source]

geometry.procrustes module

geometry.procrustes.best_orthogonal_transform(X, Y)[source]

Finds the best orthogonal transform R between X and Y, such that R X ~= Y.

geometry.procrustes.best_similarity_transform(X, Y)[source]

Finds the best transform (R,t) between X and Y, such that R X + t ~= Y.

geometry.procrustes.closest_orthogonal_matrix(M)[source]

Finds the closest orthogonal matrix to M.

geometry.rotations module

Contains all about rotation matrices, quaternions, and various conversions.

conventions: q=( a + bi + cj + dk), with a>0

geometry.rotations.SO2_from_angle(theta)[source]

Returns a 2x2 rotation matrix.

geometry.rotations.angle_from_SO2(R)[source]
geometry.rotations.angle_from_rot2d(R)
geometry.rotations.axis_angle_from_quaternion(q)[source]

This is the inverse of quaternion_from_axis_angle().

geometry.rotations.axis_angle_from_rotation(R)[source]

Returns the (axis,angle) representation of a given rotation.

There are a couple of symmetries:

  • By convention, the angle returned is nonnegative.
  • If the angle is 0, any axis will do. In that case, default_axis() will be returned.
geometry.rotations.check_SO(x)[source]

Checks that the given value is a rotation matrix of arbitrary size.

geometry.rotations.check_orthogonal(x)[source]

Check that the argument is an orthogonal matrix.

geometry.rotations.check_skew_symmetric(x)[source]

Check that the argument is a skew-symmetric matrix.

geometry.rotations.geodesic_distance_for_rotations(R1, R2)[source]

Returns the geodesic distance between two rotation matrices.

It is computed as the angle of the rotation R_1^{*} R_2^{-1}`.

geometry.rotations.hat_map(v)[source]

Maps a vector to a 3x3 skew symmetric matrix.

geometry.rotations.hat_map_2d(omega)[source]
geometry.rotations.map_hat(H)[source]

The inverse of hat_map().

geometry.rotations.map_hat_2d(W)[source]
geometry.rotations.quaternion_from_axis_angle(axis, angle)[source]

Computes a quaternion corresponding to the rotation of angle radians around the given axis.

This is the inverse of axis_angle_from_quaternion().

geometry.rotations.quaternion_from_rotation(R)[source]

Converts a rotation matrix to a quaternion.

This is the robust method mentioned on wikipedia:

<http://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation>

TODO: add the more robust method with 4x4 matrix and eigenvector

geometry.rotations.random_orthogonal_transform()[source]
geometry.rotations.random_quaternion()[source]

Generate a random quaternion.

Uses the algorithm used in Kuffner, ICRA‘04.

geometry.rotations.random_rotation(ndim=3)[source]

Generate a random rotation matrix.

This is a wrapper around random_quaternion().

geometry.rotations.rot2d(theta)

Returns a 2x2 rotation matrix.

geometry.rotations.rot2d_from_angle(theta)

Returns a 2x2 rotation matrix.

geometry.rotations.rotation_from_axes_spec(x_axis, vector_on_xy_plane)[source]

Creates a rotation matrix from the axes. x_axis is the new direction of the (1,0,0) vector after this rotation. vector_on_xy_plane is a vector that must end up in the (x,y) plane after the rotation.

That is, it holds that:

R = rotation_from_axes_spec(x, v)
dot(R,x) == [1,0,0]
dot(R,v) == [?,?,0]

TODO: add exception if vectors are too close.

geometry.rotations.rotation_from_axis_angle(axis, angle)[source]

Computes the rotation matrix from the (axis,angle) representation using Rodriguez’s formula.

geometry.rotations.rotation_from_axis_angle2(axis, angle)[source]

Get the rotation from the (axis,angle) representation.

This is an alternative to rotation_from_axis_angle() which goes through the quaternion representation instead of using Rodrigues’ formula.

geometry.rotations.rotation_from_quaternion(x)[source]

Converts a quaternion to a rotation matrix.

geometry.rotations.rotz(theta)[source]

Returns a 3x3 rotation matrix corresponding to rotation around the z axis.

geometry.rotations_embedding module

geometry.rotations_embedding.SO2_project_from_SO3(b)[source]
geometry.rotations_embedding.SO3_from_SO2(a)[source]
geometry.rotations_embedding.so2_project_from_so3(b)[source]
geometry.rotations_embedding.so3_from_so2(a)[source]

geometry.spheres module

geometry.spheres.any_distant_direction(s)[source]

Returns a direction distant from both s and -s.

geometry.spheres.any_orthogonal_direction(s)[source]

Returns any axis orthogonal to s (not necessarily random).

geometry.spheres.assert_orthogonal(s, v)[source]

Checks that two vectors are orthogonal.

geometry.spheres.default_axis()[source]

Returns the axis to use when any will do.

For example, the identity is represented by a rotation of 0 degrees around any axis. If an (axis,angle) representation is requested, the axis will be given by default_axis().

geometry.spheres.default_axis_orthogonal()[source]

Returns an axis orthogonal to the one returned by default_axis().

Use this when you need a couple of arbitrary orthogonal axes.

geometry.spheres.directions(X)[source]

Checks that every column has unit length.

geometry.spheres.distances_from(S, s)[source]

Returns the geodesic distances on the sphere from a set of points S to a given point s.

geometry.spheres.distribution_radius(S)[source]

Returns the radius of the given directions distribution.

The radius is defined as the minimum r such that there exists a point s in S such that all distances are within r from s.

\textsf{radius} = \min \{ r | \exists s : \forall x \in S : d(s,x) <= r \}

geometry.spheres.geodesic_distance_on_sphere(s1, s2)[source]

Returns the geodesic distance between two points on the sphere.

geometry.spheres.normalize_pi(x)[source]

Normalizes the entries in x in the interval [-pi,pi).

geometry.spheres.normalize_pi_scalar(x)[source]
geometry.spheres.project_vectors_onto_sphere(S, atol=1e-07)[source]
geometry.spheres.random_direction(ndim=3)[source]

Generates a random direction in S^{n-1}.

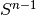Currently only implemented for 2D and 3D.

geometry.spheres.random_directions(N, ndim=3)[source]

Returns a set of random directions.

geometry.spheres.random_directions_bounded(ndim, radius, num_points, center=None)[source]

Returns a random distribution of points in 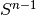S^{n-1}. within a certain radius from the point center.

The points will be distributed uniformly in that area of the sphere. If center is not passed, it will be a random direction.

geometry.spheres.random_orthogonal_direction(s)[source]

Returns a random axis orthogonal to s (only implemented for circle and sphere).

geometry.spheres.slerp(s1, s2, t)[source]

Spherical interpolation between two points on a hypersphere.

geometry.spheres.sorted_directions(S, num_around=15)[source]

Rearranges the directions in S in a better order for visualization.

In 2D, sorts the directions using their angle.

In 3D, it tries to do a pleasant elicoidal arrangement with num_around spires.

geometry.spheres.sphere_area(r=1)[source]

Returns the area of a sphere of the given radius.

geometry.spheres.spherical_cap_area(cap_radius)[source]

Returns the area of a spherical cap on the unit sphere of the given radius.

See figure at http://mathworld.wolfram.com/SphericalCap.html

geometry.spheres.spherical_cap_with_area(cap_area)[source]

Returns the radius of a spherical cap of the given area.

See http://www.springerlink.com/content/3521h167300g7v62/

geometry.spheres.unit_length(x)[source]

Checks that the value is a 1D vector with unit length in the 2 norm.

geometry.spheres_embedding module

geometry.spheres_embedding.S1_project_from_R2(b)[source]
geometry.spheres_embedding.S1_project_from_S2(b)[source]
geometry.spheres_embedding.S2_from_S1(a)[source]
geometry.spheres_embedding.S2_project_from_R3(b)[source]

geometry.tex module

geometry.yaml module

class geometry.yaml.Representation[source]

Bases: object

Methods

from_yaml  
to_yaml  
from_yaml(y)[source]
to_yaml(x)[source]
class geometry.yaml.SE3_m44[source]

Bases: geometry.yaml.Representation

Methods

from_yaml  
to_yaml  
static from_yaml()[source]
static to_yaml()[source]
class geometry.yaml.TSE3_bt[source]

Bases: geometry.yaml.Representation

Methods

from_yaml  
to_yaml  
static from_yaml()[source]
static to_yaml()[source]
geometry.yaml.from_yaml(x)[source]
geometry.yaml.get_default_representation(manifold)[source]
geometry.yaml.register_yaml_converter(manifold_name, representation, converter)[source]
class geometry.yaml.se3_m44[source]

Bases: geometry.yaml.Representation

Methods

from_yaml  
to_yaml  
static from_yaml()[source]
static to_yaml()[source]
geometry.yaml.to_yaml(manifold, value, representation=None)[source]

Module contents